In cooperative multi-agent reinforcement studying (MARL), as a result of its on-policy nature, coverage gradient (PG) strategies are sometimes believed to be much less pattern environment friendly than worth decomposition (VD) strategies, that are off-policy. Nonetheless, some recent empirical studies reveal that with correct enter illustration and hyper-parameter tuning, multi-agent PG can obtain surprisingly strong performance in comparison with off-policy VD strategies.
Why might PG strategies work so properly? On this put up, we’ll current concrete evaluation to point out that in sure eventualities, e.g., environments with a extremely multi-modal reward panorama, VD could be problematic and result in undesired outcomes. In contrast, PG strategies with particular person insurance policies can converge to an optimum coverage in these circumstances. As well as, PG strategies with auto-regressive (AR) insurance policies can study multi-modal insurance policies.
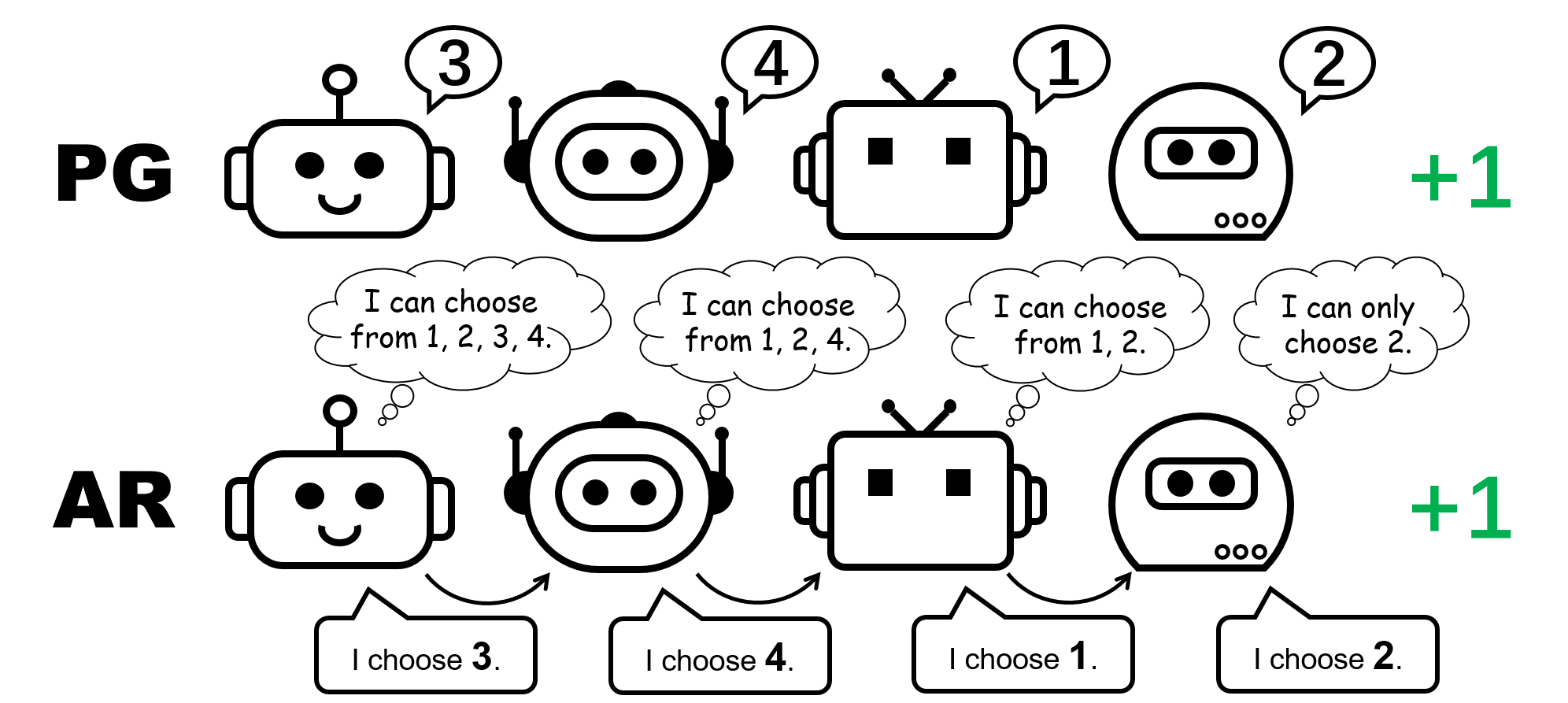
Determine 1: totally different coverage illustration for the 4-player permutation recreation.
CTDE in Cooperative MARL: VD and PG strategies
Centralized coaching and decentralized execution (CTDE) is a well-liked framework in cooperative MARL. It leverages international info for more practical coaching whereas holding the illustration of particular person insurance policies for testing. CTDE could be carried out by way of worth decomposition (VD) or coverage gradient (PG), main to 2 various kinds of algorithms.
VD strategies study native Q networks and a mixing operate that mixes the native Q networks to a world Q operate. The blending operate is normally enforced to fulfill the Particular person-World-Max (IGM) precept, which ensures the optimum joint motion could be computed by greedily selecting the optimum motion domestically for every agent.
In contrast, PG strategies straight apply coverage gradient to study a person coverage and a centralized worth operate for every agent. The worth operate takes as its enter the worldwide state (e.g., MAPPO) or the concatenation of all of the native observations (e.g., MADDPG), for an correct international worth estimate.
The permutation recreation: a easy counterexample the place VD fails
We begin our evaluation by contemplating a stateless cooperative recreation, specifically the permutation recreation. In an $N$-player permutation recreation, every agent can output $N$ actions ${ 1,ldots, N }$. Brokers obtain $+1$ reward if their actions are mutually totally different, i.e., the joint motion is a permutation over $1, ldots, N$; in any other case, they obtain $0$ reward. Be aware that there are $N!$ symmetric optimum methods on this recreation.
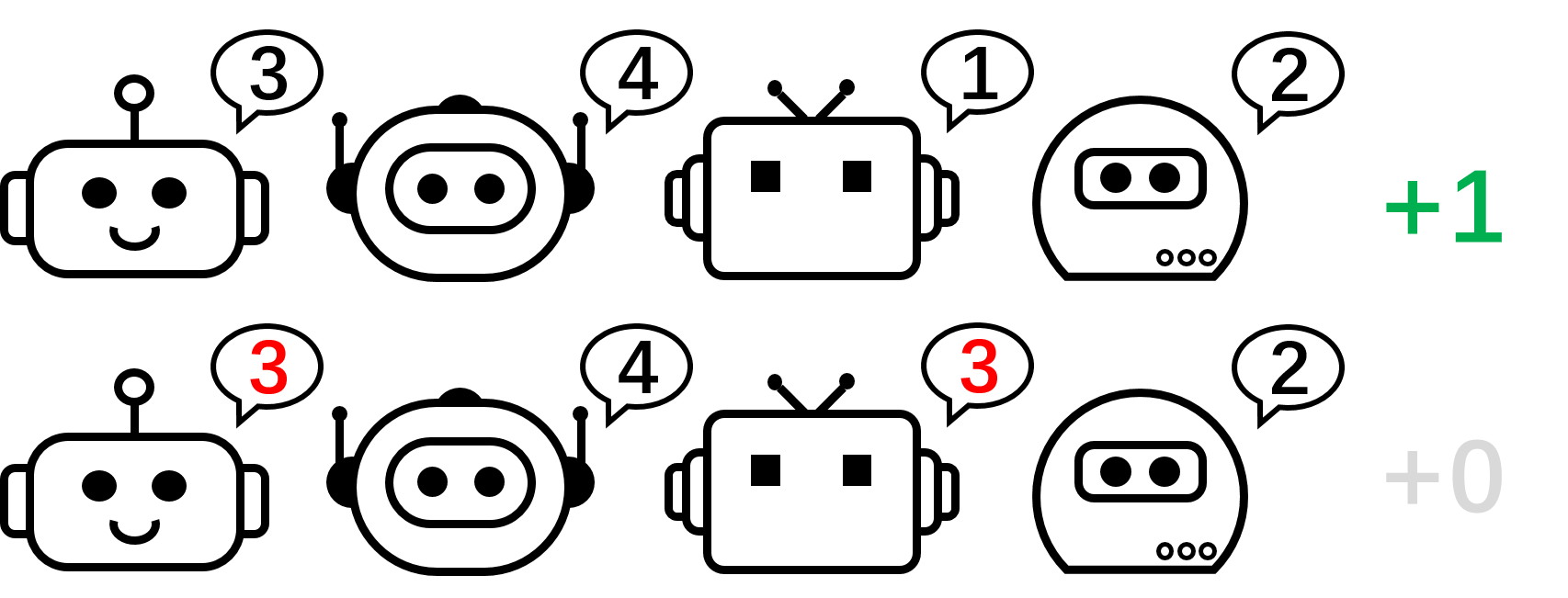
Determine 2: the 4-player permutation recreation.
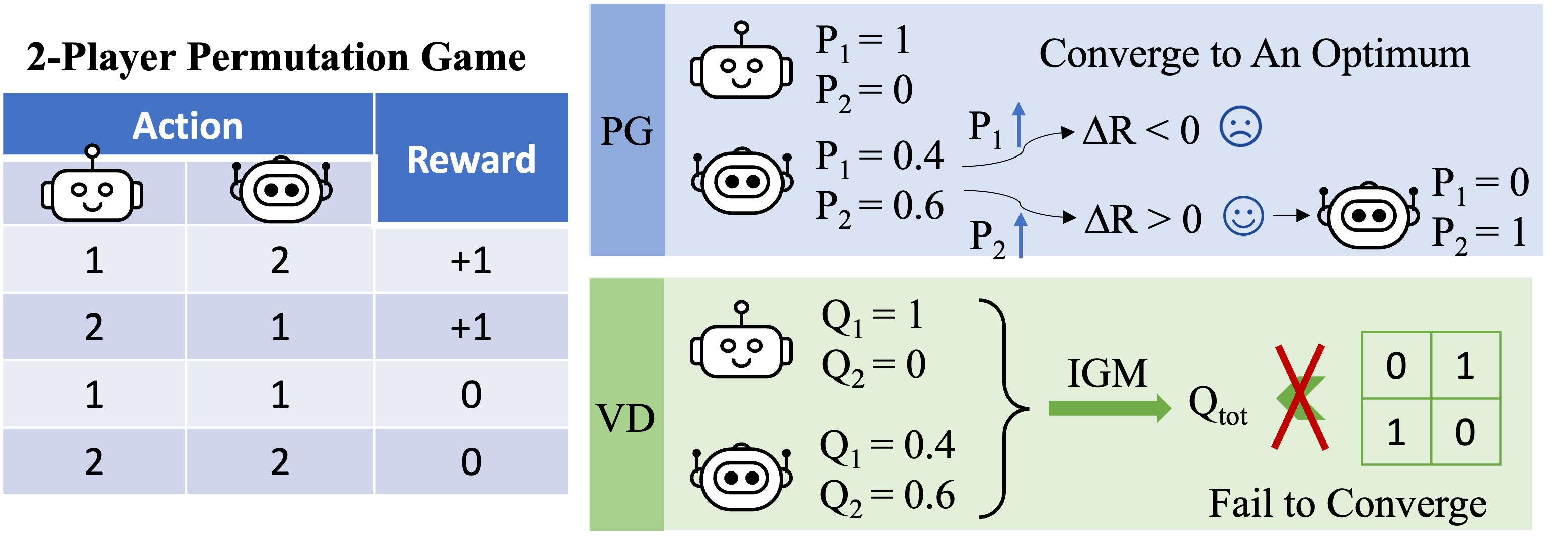
Determine 3: high-level instinct on why VD fails within the 2-player permutation recreation.
Allow us to deal with the 2-player permutation recreation now and apply VD to the sport. On this stateless setting, we use $Q_1$ and $Q_2$ to indicate the native Q-functions, and use $Q_textrm{tot}$ to indicate the worldwide Q-function. The IGM precept requires that
[argmax_{a^1,a^2}Q_textrm{tot}(a^1,a^2)={argmax_{a^1}Q_1(a^1),argmax_{a^2}Q_2(a^2)}.]
We show that VD can not signify the payoff of the 2-player permutation recreation by contradiction. If VD strategies had been in a position to signify the payoff, we’d have
[Q_textrm{tot}(1, 2)=Q_textrm{tot}(2,1)=1quad text{and}quad Q_textrm{tot}(1, 1)=Q_textrm{tot}(2,2)=0.]
If both of those two brokers has totally different native Q values (e.g. $Q_1(1)> Q_1(2)$), we’ve $argmax_{a^1}Q_1(a^1)=1$. Then in response to the IGM precept, any optimum joint motion
[(a^{1star},a^{2star})=argmax_{a^1,a^2}Q_textrm{tot}(a^1,a^2)={argmax_{a^1}Q_1(a^1),argmax_{a^2}Q_2(a^2)}]
satisfies $a^{1star}=1$ and $a^{1star}neq 2$, so the joint motion $(a^1,a^2)=(2,1)$ is sub-optimal, i.e., $Q_textrm{tot}(2,1)<1$.
In any other case, if $Q_1(1)=Q_1(2)$ and $Q_2(1)=Q_2(2)$, then
[Q_textrm{tot}(1, 1)=Q_textrm{tot}(2,2)=Q_textrm{tot}(1, 2)=Q_textrm{tot}(2,1).]
Because of this, worth decomposition can not signify the payoff matrix of the 2-player permutation recreation.
What about PG strategies? Particular person insurance policies can certainly signify an optimum coverage for the permutation recreation. Furthermore, stochastic gradient descent can assure PG to converge to one in every of these optima under mild assumptions. This means that, despite the fact that PG strategies are much less common in MARL in contrast with VD strategies, they are often preferable in sure circumstances which are widespread in real-world purposes, e.g., video games with a number of technique modalities.
We additionally comment that within the permutation recreation, so as to signify an optimum joint coverage, every agent should select distinct actions. Consequently, a profitable implementation of PG should make sure that the insurance policies are agent-specific. This may be carried out by utilizing both particular person insurance policies with unshared parameters (known as PG-Ind in our paper), or an agent-ID conditioned coverage (PG-ID).
PG outperforms present VD strategies on common MARL testbeds
Going past the easy illustrative instance of the permutation recreation, we prolong our examine to common and extra life like MARL benchmarks. Along with StarCraft Multi-Agent Problem (SMAC), the place the effectiveness of PG and agent-conditioned coverage enter has been verified, we present new ends in Google Analysis Soccer (GRF) and multi-player Hanabi Challenge.
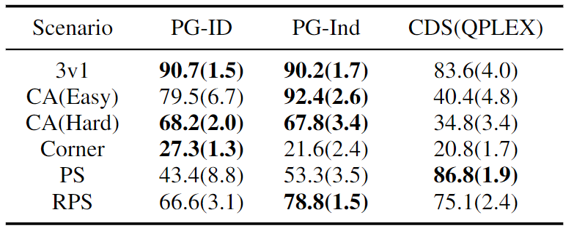
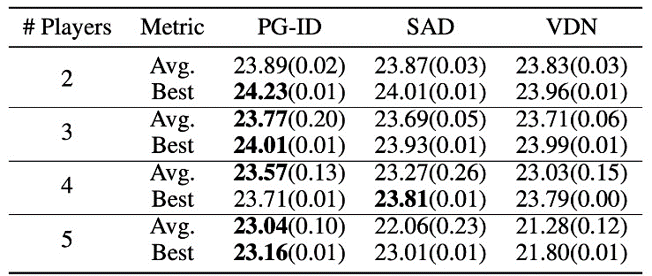
Determine 4: (left) successful charges of PG strategies on GRF; (proper) greatest and common analysis scores on Hanabi-Full.
In GRF, PG strategies outperform the state-of-the-art VD baseline (CDS) in 5 eventualities. Apparently, we additionally discover that particular person insurance policies (PG-Ind) with out parameter sharing obtain comparable, typically even increased successful charges, in comparison with agent-specific insurance policies (PG-ID) in all 5 eventualities. We consider PG-ID within the full-scale Hanabi recreation with various numbers of gamers (2-5 gamers) and evaluate them to SAD, a powerful off-policy Q-learning variant in Hanabi, and Worth Decomposition Networks (VDN). As demonstrated within the above desk, PG-ID is ready to produce outcomes similar to or higher than the very best and common rewards achieved by SAD and VDN with various numbers of gamers utilizing the identical variety of atmosphere steps.
Past increased rewards: studying multi-modal habits by way of auto-regressive coverage modeling
In addition to studying increased rewards, we additionally examine find out how to study multi-modal insurance policies in cooperative MARL. Let’s return to the permutation recreation. Though we’ve proved that PG can successfully study an optimum coverage, the technique mode that it lastly reaches can extremely depend upon the coverage initialization. Thus, a pure query will likely be:
Can we study a single coverage that may cowl all of the optimum modes?
Within the decentralized PG formulation, the factorized illustration of a joint coverage can solely signify one specific mode. Subsequently, we suggest an enhanced method to parameterize the insurance policies for stronger expressiveness — the auto-regressive (AR) insurance policies.

Determine 5: comparability between particular person insurance policies (PG) and auto-regressive insurance policies (AR) within the 4-player permutation recreation.
Formally, we factorize the joint coverage of $n$ brokers into the type of
[pi(mathbf{a} mid mathbf{o}) approx prod_{i=1}^n pi_{theta^{i}} left( a^{i}mid o^{i},a^{1},ldots,a^{i-1} right),]
the place the motion produced by agent $i$ relies upon by itself commentary $o_i$ and all of the actions from earlier brokers $1,dots,i-1$. The auto-regressive factorization can signify any joint coverage in a centralized MDP. The solely modification to every agent’s coverage is the enter dimension, which is barely enlarged by together with earlier actions; and the output dimension of every agent’s coverage stays unchanged.
With such a minimal parameterization overhead, AR coverage considerably improves the illustration energy of PG strategies. We comment that PG with AR coverage (PG-AR) can concurrently signify all optimum coverage modes within the permutation recreation.

Determine: the heatmaps of actions for insurance policies realized by PG-Ind (left) and PG-AR (center), and the heatmap for rewards (proper); whereas PG-Ind solely converge to a selected mode within the 4-player permutation recreation, PG-AR efficiently discovers all of the optimum modes.
In additional complicated environments, together with SMAC and GRF, PG-AR can study attention-grabbing emergent behaviors that require robust intra-agent coordination which will by no means be realized by PG-Ind.
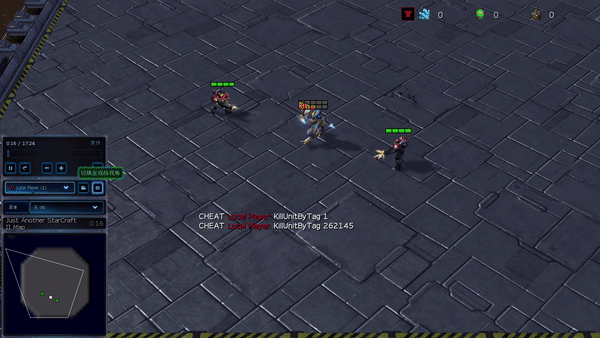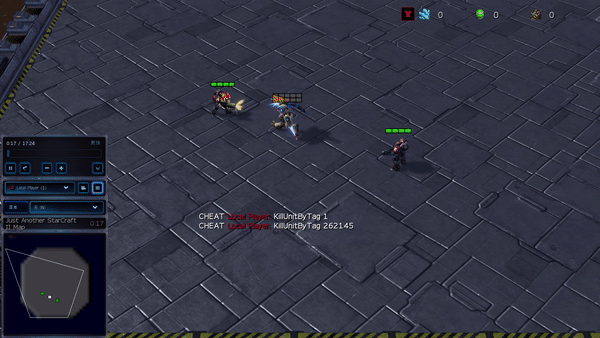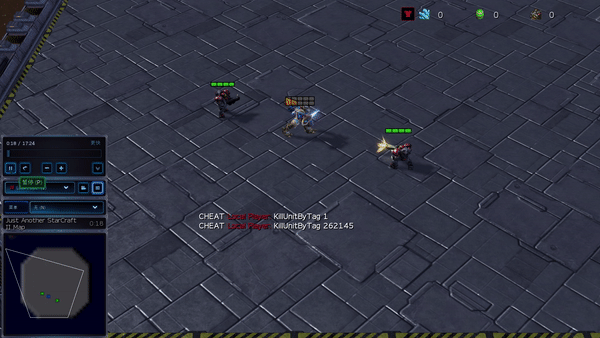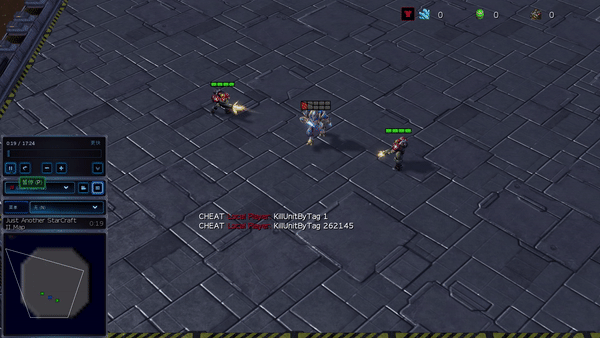
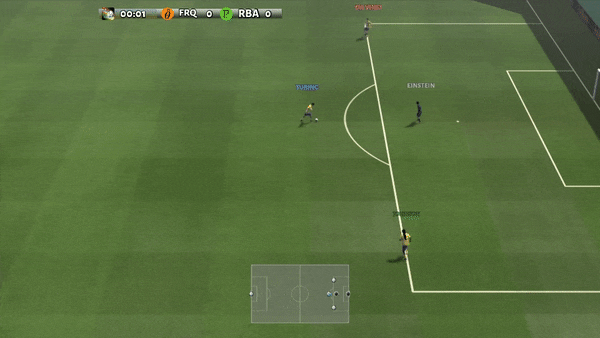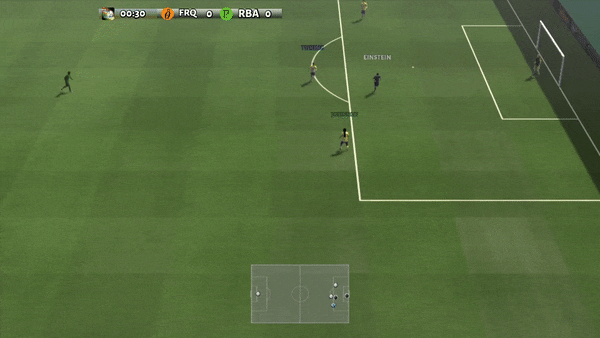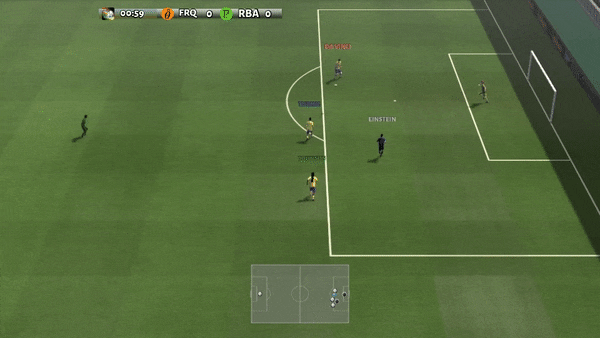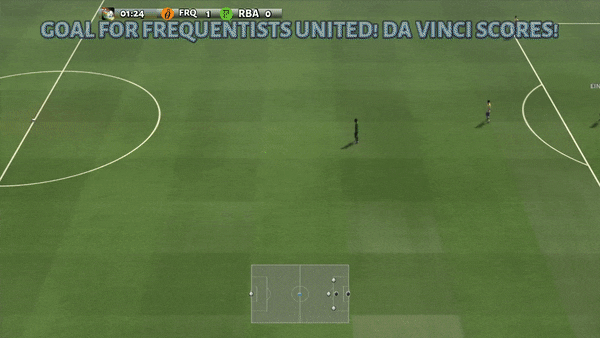
Determine 6: (left) emergent habits induced by PG-AR in SMAC and GRF. On the 2m_vs_1z map of SMAC, the marines maintain standing and assault alternately whereas making certain there is just one attacking marine at every timestep; (proper) within the academy_3_vs_1_with_keeper state of affairs of GRF, brokers study a “Tiki-Taka” fashion habits: every participant retains passing the ball to their teammates.
Discussions and Takeaways
On this put up, we offer a concrete evaluation of VD and PG strategies in cooperative MARL. First, we reveal the limitation on the expressiveness of common VD strategies, exhibiting that they might not signify optimum insurance policies even in a easy permutation recreation. In contrast, we present that PG strategies are provably extra expressive. We empirically confirm the expressiveness benefit of PG on common MARL testbeds, together with SMAC, GRF, and Hanabi Problem. We hope the insights from this work may gain advantage the group in direction of extra basic and extra highly effective cooperative MARL algorithms sooner or later.
This put up relies on our paper: Revisiting Some Widespread Practices in Cooperative Multi-Agent Reinforcement Studying (paper, website).








